Running a Kruskal-Wallis (nonparametric) ANOVA in Stata
Sometimes, for whatever reason, your data is not normal - a fundamental assumption for the standard ANOVA. While the ANOVA is robust over moderate violations of the assumption, there will come a time when it is better to run a nonparametric ANOVA. There are, however, certain limitations to the nonparametric ANOVA: first and foremost, you need to have sample sizes as close to equal as possible (though the Kruskal-Wallis ANOVA is also robust over small differences). Kruskal-Wallis does assume that the distributions of the groups are approximately equal (so if one set of data was skewed to the right and one to the left, you would not be able to run a Kruskal-Wallis ANOVA. Finally, you cannot easily run post-hoc analyses in cases with more than two groups (though if there is only one factor you could do follow-up Mann-Whitney U tests and adjust the p-value for the number of comparisons you're doing).
To learn a bit more about the theory behind a Kruskall-Wallis ANOVA click here. Otherwise, see the instructions below.
Running a Kruskal-Wallis test does not require the data to be arranged in any special way. As long as you have a grouping variable, the command is simply kwallis [dep var name], by([grouping var]).
For instance, if I want to look at SAT entrance scores at four colleges (similarly distributed data with a strong negative skew) the command would be kwallis SAT. by(college)
The output from such a test looks something as follows (data totally made up)
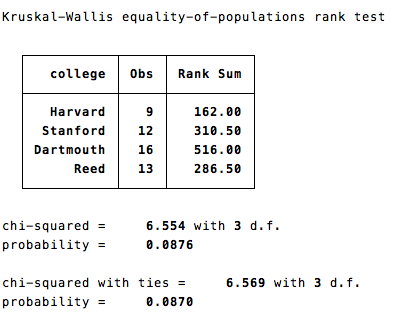
The output gives a list of the colleges in my sample, as well as the rank of each. These ranks are U-values which can then be looked up on a U-table. Alternatively you can look at the chi-square numbers below the table - the probabilities are the same (use the "ties" value one if if two of your scores are the same).
As usual, consulting the help file (help kwallis) will offer details about what options are available.