Positive Associations

Students in Math 113 investigate a curious polytope.

In standard arithmetic, multiplication is associative: the product ab times c is equal to a times the product bc, or, as an equation, (ab)c = a(bc).¹  It follows that the product of any ordered list of numbers is independent of the way in which we group pairwise multiplications. As any adept kindergartener will inform you, this is a fine and important conclusion to draw, but it needn’t be the end of the story. Students in Math 113: Discrete Structures consider the number of ways in which a list of n + 1 symbols can be parenthesized (with n – 1 pairs of well-matched parentheses). If n = 2, there are two ways, (ab)c and a(bc), and if n = 3 there are five ways: ((ab)c)d, (a(bc))d, a((bc)d), a(b(cd)), and (ab)(cd). In general, the number of ways is given by the nth Catalan number,

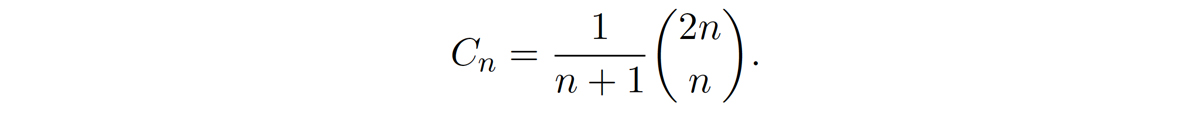
(The symbol \(\binom{2n}{n}\) is a binomial coefficient representing the number of ways to choose a committee of n from a group of 2n people.) The Swiss mathematician Leonard Euler wrote down an equivalent formula in 1751, but the proof would not appear until 1758 and included contributions from Christian Goldbach and Johann Andreas von Segner. (The Mongolian mathematician Mingantau had also discovered the formula by 1730.)

Associativity didn’t get much additional attention until Jim Stasheff and Dov Tamari revisited its basic premises in the 1950s and ’60s. They discovered a polytope (a higher-dimensional analogue of a polyhedron) called the associahedron whose vertices correspond to parenthesizations, and whose edges encode single applications of the associative law (ab)c = a(bc). This geometric generalization of one of the oldest laws in algebra appears in wild and unexpected places, including homotopy associativity of loop spaces, type A cluster algebras, higher category theory, and scattering amplitudes in string theory.

Tags: Academics, Courses We’d Love To Take, Object of Study, Professors