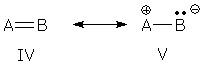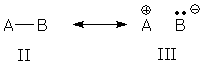
|
|

|
Resonance (superposition) affects everything Practically every wave function can be improved, at least a little, by combining it with other functions. So in this sense, every molecule is a resonance hybrid. But this is hair-splitting. What I really asking here is, "are most (or all) molecules resonance hybrids in some significant way?" Can we think about a molecule, with even a little success, without using resonance, or is resonance a universal phenomenon? Without giving away the answer, I'll just say that resonance is much more widespread than most chemists realize. To convince you of this, I will describe two widely encountered electron patterns that seem to involve resonance: polar covalent bonds and nonpolar covalent bonds. A word of warning -- modern chemists do not refer to localized bonds as resonance hybrids. However, Pauling described them as resonance hybrids and it may help you understand bonds better if you think about them (even briefly) the way he did.
Polar covalent bonds The AB bond represented by forms IV and V is a partial double bond. Charge separation in V shows that the bond has polar character. This kind of bond appears in the many groups -- C=O, CN (double and triple), and N=O -- and organic chemists unanimous agree that these groups are resonance hybrids.
The AB bond represented by forms II and III looks like the same kind of superposition, but is this group a resonance hybrid?
Once upon a time, II/III resonance was called no-bond resonance (because III lacks a bond) and AB was viewed as a resonance hybrid. However, chemists somehow lost interest/awareness of this description and stopped talking about it and teaching it. Now, instead of calling AB a resonance hybrid, they say the AB bond is a localized covalent bond with polar character. Chemists can deny the existence of no-bond resonance if they like, but their so-called "localized polar covalent bond" is identical to no-bond resonance. To prove this, I'll construct a superposition of II and III. As usual, I begin by writing the wave function for each resonance form: WF(II) = BO(AB) = AO(A) + AO(B) WF(III) = AO(B) Then I make a superposition of these forms: WFsuper = WF(II) + nWF(III) = AO(A) + AO(B) + nAO(B) = AO(A) + (1 + n)AO(B) The last line shows that the II/III superposition (no-bond resonance) is equivalent to a polar bond orbital dominated by atom B, i.e., II/III resonance produces a localized (?) polar covalent bond. The "localized polar covalent bond" picture has one advantage: it saves us from drawing resonance forms for every polar covalent bond. However, the "localized" picture also has two significant disadvantages. It hides the factors that lead to polar bonding: a small energy gap between forms II and III, and strong interaction between these forms. And it encourages us to give different labels to similar patterns (IV/V vs. II/III).
Nonpolar covalent bonding The covalent bond in H2 is nonpolar, and Pauling suggested that it should be viewed as a superposition of resonance forms IX and X:
(Let me clarify the meaning of these drawings. IX shows the "blue" electron near the left-hand H nucleus and the "red" electron near the right-hand H nucleus. The electrons have swapped places in X. Forms IX and X "localize" one electron near each atomic nucleus. Electron "sharing" (delocalization) doesn't occur until we superposition IX and X.) In support of his argument, Pauling calculated the energy of resonance form IX for several HH distances. E(IX) does not behave at all like the energy of H2. On the other hand, Esuper does behave realistically. It seems plausible that a superposition of IX and X might be a better wave function than either IX or X alone. IX and X have the same energy, one of our conditions for effective superposition. And, IX and X interact strongly when the HH distance is short, our second condition for effective superposition. If we focus on the "blue" electron, we find: WF(IX) = AO(Hleft) WF(X) = AO(Hright) WFsuper = AO(Hleft) + AO(Hright) = BO(HH) The delocalization created by resonance between IX and X is equivalent to the delocalization created by a bond orbital. Without delocalization (resonance), there isn't any bond.
Summary Covalent bonds, both polar and nonpolar, should be viewed as a superposition of simpler wave functions. The superpositions can be constructed using different terminology. If we combine resonance forms, we obtain a resonance hybrid. On the other hand, if we combine atomic orbitals, we obtain bond orbitals. These pictures may use different terminology, but they lead to the same wave functions, and both confirm the fundamental role played by superposition in chemical bonding. |