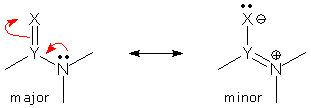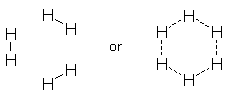
|
|

|
Resonance affects molecular geometry Electron delocalization frequently reveals itself through a distorted molecular geometry. The most frequently cited situation is a symmetric set of bond distances in a molecule that does not have a symmetric Lewis structure, but delocalization can also create other kinds of geometrical distortions. The first two sections in this essay examine distortions in bond distances and bond angles. The last section looks at recent research on the "real" factors that make benzene (and possibly many other molecules) symmetric. Bond Distances | Bond Angles | Benzene
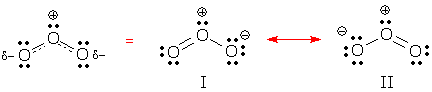
Ozone, O3, is an excellent example of a symmetrical resonance hybrid with distorted bond distances. If ozone was a normal molecule with localized bonds, that is, if it was adequately described by Lewis structure I, we might expect to find one short OO bond of ~122 pm (this distance is observed in O=O [1]) and one long bond of ~147 pm (this distance is observed in HO-OH).
As it happens, the OO distances in ozone are identical, and at 128 pm, they tends toward "short", but we could call them "in between." To explain these observations, chemists say ozone's electron pattern is a "hybrid" of resonance forms I and II as shown in the dashed-line formula on the left, and ozone's geometry reflects its partial double bonds. This kind of analysis is applied to all resonance hybrids. We always expect a hybrid's bond distances to reflect the hybrid's bond pattern. If the hybrid contains a partial double bond, the bond distance should be somewhat longer than a complete double bond, and somewhat shorter than a single bond. Analogous predictions would be made for partial single bonds and partial triple bonds.
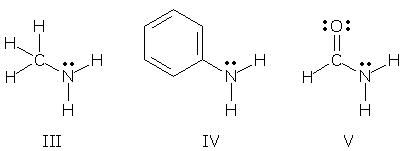
VSEPR rules link bond angles to the number of electron pairs surrounding an atom. 4 pairs imply a tetrahedral atom with bond angles of ~109o, 3 pairs imply a trigonal atom with bond angles of 120o, and 2 pairs imply a linear atom. The counting of electron pairs, and the prediction of bond angles, becomes uncertain when a lone pair is delocalized. (VSEPR rules treat "lone pair + sigma bond pair" as two electron pairs, and "sigma bond pair + pi bond pair" as only one; a delocalized lone pair with partial pi bonding properties falls somewhere in between.) Therefore, a resonance hybrid with a delocalized lone pair may display distorted bond angles. Consider the N atoms in compounds III-V. These atoms have 4 electron pairs, one of which is a lone pair. We expect to see tetrahedral bond angles of ~109.5o if the lone pair electrons are localized on N.
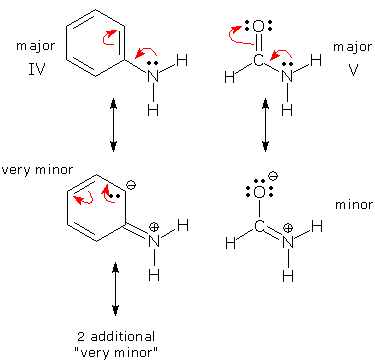
Molecular models show that only one N (compound III) is tetrahedral (angles = 109.6, 109.6, 105.8o). The N in compound V is trigonal (angles = 121.8, 119.2, 119.0o) and the N in compound IV is somewhere "in between" (angles = 114.6, 114.6, 111.0o). Distorted bond angles like these indicate that IV and V may be resonance hybrids with delocalized lone pairs. More information can be obtained by looking at CN bond distances. Compound III, with its normal bond angles, also contains a normal CN single bond: 146 pm. The CN bond in compound V (trigonal N) is much shorter: 136 pm. And the CN bond in compound IV ("in between" N) is somewhere "in between": 140 pm. These data suggest that the CN bonds in V and IV have some partial double bond character, consistent with delocalization of the N lone pair. These ideas can be described by the resonance forms shown below. Compound V's bond angles and distances are highly distorted, so its minor form must make an appreciable contribution. Compound IV's geometry is closer to normal, and its minor forms must make a smaller contribution. (You might have anticipated that "minor" V would be more important than "very minor" IV because "minor" V places negative charge on electronegative O, while "very minor" IV places it on C.)
Compounds IV and V show how misleading a single Lewis structure can be. If we didn't know the geometries of these compounds, we might never have suspected these compounds of being resonance hybrids. However, now that we know these compounds are resonance hybrids, we can be on the "look out" for other similar compounds. Any time a N (equipped with a lone pair) lies next to a pi system, it may be possible to delocalize the N lone pair by converting it into a pi bond pair.
Revised VSEPR: partial electron domains. If you try to apply VSEPR to the superposition shown above, you will probably get confused. The major form with an N lone pair shows 4 electron domains around N, while the minor form with a YN double bond shows just 3. The hybrid is a single molecule with a single geometry; how can this be consistent with two different electron domain values? To solve this problem, we might pay attention to the fact that the YN bond domain exists in both forms, but the N lone pair domain does not. We might think of the latter as a partial domain, making the total number of N domains fall somewhere between 4 and 3. (Note: for reasons that I won't go into here, the N lone pair domain effectively vanishes even when the "Y=N" form is only a minor form. One can do well by ignoring delocalized lone pairs when counting electron domains.)
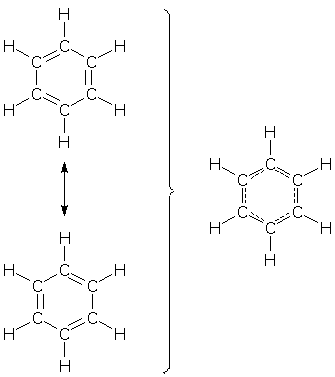
(Every now and then, someone announces that the "theory of chemistry" is complete. Whoever thinks this is true might consider this next story...) Several lines of evidence identify benzene as a resonance hybrid. One of these is benzene's symmetric geometry. All 6 CC bond distances are identical, and at 140 pm they lie in between the distances observed for normal CC single bonds (153 pm) and double bonds (134 pm).
Chemists expect a hybrid's bond distances to reflect its bond pattern. In the case of benzene, a partial double bond should produce an "in between" bond distance. Chemists have noted for a long time that benzene's symmetric geometry is ideal from another point-of-view: the symmetric geometry makes the energies of the resonance forms identical, the precise condition needed to create maximum energy stabilization (see Resonance Effects on Energy). Based on this (correct!) analysis, chemists then jumped to a logical, but incorrect conclusion: benzene is symmetric because of electron delocalization and the energy gain it provides. Beginning in the 1980's, two chemists, Sason Shaik of Israel and Philippe Hiberty of France, published a series of research papers that showed that the conventional wisdom regarding benzene's geometry cannot be true. Their counter-theory, which is now supported by several kinds of experimental and computational evidence, shows that it would be better (energetically) for benzene if its pi electrons remained localized in 3 short double bonds instead of delocalizing to form 6 long partial double bonds. Their theory also identifies benzene's localized sigma bonds as the real driving force behind benzene's symmetric geometry; the sigma bonds benefit greatly from identical CC bond distances. How can 3 short double bonds be preferred when a symmetric geometry provides maximum pi electron delocalization and stabilization? The answer to this paradox lies in the two factors that contribute to electron energy (see Resonance Effects on Energy): Esuper = Ewrong + interactions When benzene moves from a "3 short double bond" geometry to a symmetric geometry, two things happen simultaneously: stabilizing interactions are maximized because electron delocalization is maximized, but Ewrong is destabilized because the symmetric geometry is far from ideal for the double bond pattern seen in each resonance form. Ewrong turns out to be the deciding factor. Hence, Shaik and Hiberty's conclusion: it would be better for benzene if its pi electrons remained localized in 3 short double bonds. This theory may seem strange (it has yet to find its way into chemistry textbooks), but one can easily find analogous systems that prefer localized bonds over delocalized ones.
The old argument might have suggested that 6 H atoms would form an H6 resonance hybrid with 6 identical delocalized bonds (see above), but it is well known that they prefer to form 3 H2 molecules with 3 short localized bonds. Shaik and Hiberty's analysis of benzene almost certainly applies to other resonance hybrids. One can only wonder what chemistry textbooks will look like 50 years from now. [1] OO does not contain a double bond in its ground state. The cited distance is observed in the first excited singlet state, which does contain a double bond. [back]
|