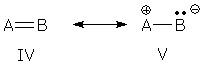
ROCO Resonance: Wave Functions

This essay contains information that I have never found in any organic chemistry textbook. This can mean two things: the information is too difficult or you don't really need to know it. Maybe both are true. In any case, you don't have to read this essay in order to use resonance successfully. I wrote it mainly to scratch an itch that has been bothering me since the early '90s.

When Linus Pauling developed resonance theory, he defined "resonance" as the superposition of wave functions. Unfortunately, this detail has been lost in the intervening decades, and modern chemists incorrectly treat "resonance" as the superposition of Lewis structures (resonance forms).

The distinction between wave function and Lewis structure is a subtle one, and this probably explains why the modern error has been perpetuated for so long. In this essay, I try to explain how one can view a Lewis structure as a wave function, and how this affects the prediction of molecular properties.

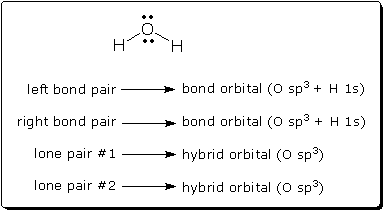
A Lewis structure is a drawing consisting of symbols for bond pairs and lone pairs. A wave function is a mathematical formula consisting of orbitals. [1] What could these have in common?

Obviously, Lewis structures and wave functions both describe electrons, but the similarity goes deeper. A Lewis structure can, in fact, be translated directly into a specific wave function. And this translation is a necessary step when one uses resonance theory.

To see how one translates a Lewis structure into a wave function, consider a simple molecule like water. As the following diagram shows, every electron pair in the Lewis structure corresponds to a specific doubly-occupied orbital in the wave function. If we know how to draw the Lewis structure, we know how to write the wave function, and vice versa.

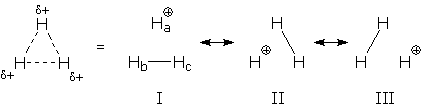
The same kind of "Lewis structure = wave function" idea can be applied to resonance forms (which is what Pauling intended). First, we translate each form into its corresponding wave function. Then, we superposition the wave functions to generate the resonance hybrid's wave function.

I'll illustrate this procedure for H3+. This ion is shaped like an equilateral triangle, which indicates three identical HH bonds. Since the ion contains only two electrons, it must be a resonance hybrid:

Each resonance form contains one electron pair, a bond pair between two H. In wave function language, each form corresponds to a doubly-occupied HH bond orbital (BO). If we write these bond orbitals as bonding combinations of H 1s orbitals, and label the 1s orbitals, we can see the differences between these wave functions:

Next, we construct a superposition of these wave functions. This gives the hybrid's wave function:

If we substitute the definitions of each BO into this formula, we can get a formula for BO(hybrid) in terms of H 1s orbitals:

Notice that the hybrid's wave function looks like a bond orbital, except that it is delocalized. Instead of combining orbitals from two atoms, like a normal bond orbital, BO(hybrid) combines orbitals from three atoms. When this delocalized orbital is occupied, it simultaneously creates three partial, identical HH bonds. The standard resonance drawing is equivalent to the more convoluted mathematical treatment. Amazing.

Now that you can see how "superposition of wave functions" (i.e., resonance) works, I'll explain why it is important to use this approach when predicting molecular properties.

There are two ways to predict the properties of a resonance hybrid. One method is widely taught and used (I used it myself in my essay on resonance contributors when I predicted the properties of ozone), but is wrong. The other is correct, but can be much harder to use. I can best illustrate this with a simple example (and a little math).

The usual (wrong) prediction procedure. The usual procedure says, "combine what you see in each Lewis structure." In other words, combine the electron density (ED) on A in form IV with the electron density on A in form V:

(The "1/2" tells you I am assuming IV and V contribute equally. This assumption is not required, but it makes the formulas in this essay easier to read and think about.)

The much-ignored (correct) prediction procedure. You may recall that electron density (ED) is given by the square of the wave function (WF). If we want to know the electron density on A, we must look at the square of the wave function near A:

Wave functions seem like mysterious beasts, but we know that this molecule is a resonance hybrid, so its wave function is a superposition of wave functions: [2]

The final formula shows the discrepancy between the right answer, ED(hybrid), and the usual (wrong) answer, EDwrong. The correct formula includes WF(IV)WF(V). This term is called the "interaction density" or "overlap density," and is a product of two different wave functions. The interaction density affects the electron density everywhere in the molecule, and its appearance tells us that the electron density obtained by the "usual" procedure is wrong.

Electron density is just one of many properties that interest chemists, but all property predictions -- electron density, bond type, atom charge, dipole moment, geometry, energy, etc. -- have something in common with electron density prediction: the prediction procedure must start with WF(hybrid), and their answers always include interaction terms. In fact, we can draw an analogy between the ED(hybrid) formulas given above and other property formulas. In general, a hybrid's property will be given by:

where propertywrong refers to the property obtained by combining the properties of individual resonance forms.

Chemists use the usual/wrong prediction method because it is usually convenient and tempting to do so.

First, interaction terms are hard to estimate. Second, they can be small, although there is no guarantee on this score. Third, we usually aren't that interested in an accurate answer. These factors all encourage us to ignore inconvenient interaction terms and take propertywrong as the right answer.

I am as guilty in this as the next chemist. As I mentioned at the start of this essay, I used the wrong procedure in another essay to estimate atom charges and bond types for ozone because this is standard practice.

In another essay I will show you that interaction terms cannot be ignored during energy predictions, and chemists routinely take interaction energies into account.

[1] This statement is correct for model wave functions only, and not for the real wave function. [back]
[2] The scaling factor, 0.707, is not correct, but it makes the equations a little cleaner. The correct scaling factor leads to the same conclusion regarding interaction density, so just bear with me. [back]