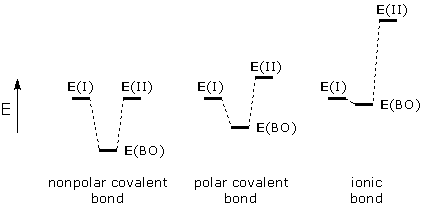
|
|

|
Superposition affects energy Fundamental questions about superposition A molecule's properties are determined by its wave function. In the case of a resonance hybrid, we write the wave function as a superposition of two simpler wave functions. Another essay describes how this leads to some surprising results for molecular formulas. The hybrid's properties are not just a superposition of resonance form propertiesThis raises an imp wave functions. This One of the best ways to construct a complicated, high quality wave function is to superposition (combine) simpler, low quality wave functions. But for this procedure to be useful, we must know:
This essay is divided into four sections. The first section answers these questions in a general way. The remaining sections then illustrate how these answers get applied to resonance hybrids, bond orbitals, and hybrid orbitals. Since several unrelated topics are covered here, you might want to skip directly to the one that interests you: general theory | resonance hybrids | bond orbitals | hybrid orbitals
Chemists construct complicated, high quality wave functions by superpositioning (combining) simple, low quality wave functions. This procedure can be summarized in words, but the techniques and vocabulary are inherently mathematical, so I will describe the procedure using this language. Suppose I have a molecule and WF(I) is a fair approximation to its wave function. This is equivalent to saying that E(I), the energy of this wave function is close to being right. My goal is to improve WF(I) by combining it with another wave function, WF(II). I will assume that the second wave function is not as good an approximation as my original. This is equivalent to assuming E(I) < E(II). [Important note: An incredibly valuable theorem in quantum mechanics says the quality of a wave function is inversely related to its energy. Higher quality equals lower energy. The best wave function, the "truth", has the lowest possible energy.] Let's call the superposition wave function, WFsuper: WFsuper = WF(I) + nWF(II) and use n to represent how much WF(II) contributes to the superposition.
What simple wave functions work best? How should we combine them? After a little "magic" math, one can show:
n is the ratio of two quantities: Eint, the interaction energy between WF(I) and WF(II), and [E(I) - E(II)], the energy gap between the two approximate wave functions. I shall assume that the energy gap is larger than the interaction energy. This gives: 0 ≤ |n| ≤ 1 (Note: this inequality holds even when my assumption is wrong because I get to use a different formula for n.) Focusing on what makes n as large as possible, we can answer the first two questions:
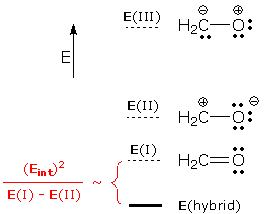
What is the energy of the resulting superposition wave function? Some more "magic" math gives Esuper, the energy of the superposition wave function. Rather than give the full formula, let me remind you of a formula I gave in the Superposition of Wave Functions essay: property(superposition) = propertywrong + interactions This formula says that the property of a superposition wave function is the sum of propertywrong (the property obtained by combining the properties of the component wave functions) and interactions (a number created by interactions between component wave functions). This formula applies to Esuper, and it says that Esuper is stabilized relative to the component energies by the following amount:
This provides an answer to our third question:
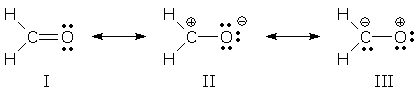
Resonance theory uses a simplified version of the energy analysis outlined above. Resonance forms correspond to WF(I) and WF(II), and the resonance hybrid corresponds to WFsuper. However, the influence of WF(II) is determined entirely by the E(I)-E(II) energy gap. The interaction energy is ignored. You can see how this works for formaldehyde, H2CO:
The lowest energy form is I (it contains more bonds, more atoms with octets, and fewer charges than the other forms). It is the major contributor. II is lower in energy than III (the latter improbably transfers electrons from O, a very electronegative atom, to C). This gives us the following energy ordering: E(I) < E(II) <<< E(III). We can ignore III because the large energy gap between I and III prevents III from contributing to the hybrid. The relative energies of the resonance forms and the actual molecule (i.e., the hybrid) are shown below. The superposition of I and II shows that the actual molecule has a lower energy than either resonance form.
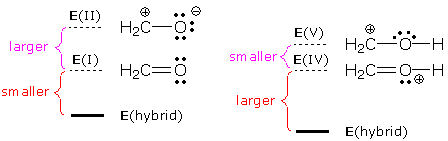
When formaldehyde is protonated, the resulting cation is also a resonance hybrid. The energies of the resonance forms and resulting hybrids are:
We predict a relatively large role for resonance form V because the IV-V energy gap is small. This enhanced role translates into large stabilization of the hybrid relative to IV. It also predicts a longer CO bond (molecular models indicate that the CO bond is ~50 pm longer than the bond in formaldehyde).
Bond orbital theory uses the complete energy analysis given above. Atomic orbitals on neighboring atoms play the roles of WF(I) and WF(II), respectively. Superpositioning (combining) these orbitals gives a bond orbital (BO) that corresponds to WFsuper. Effect of energy gap. Three possible effects of the E(I)-E(II) energy gap on BO energy and polarity are shown below:
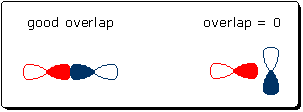
When there is a tight match between E(I) and E(II), the bond orbital is stabilized by a large amount and both atomic orbitals contribute equally (n ~ 1). This corresponds to a nonpolar covalent bond, like the CC bond in ethane, H3C-CH3. When there is a gap between E(I) and E(II), the bond orbital is less stabilized. The bond orbital also becomes polarized because n < 1 (WF(II) contributes less than WF(I)). This kind of scenario might apply to the OH bonds in water. If the energy gap is large enough, WF(II) will not contribute to BO, and the electrons in BO will reside entirely on atom I. Effect of interaction energy. The interaction energy, Eint, between two atomic orbitals is proportional to the overlap between these orbitals. This means high overlap is necessary and desirable for bond orbital formation. The following drawing shows two possible orbital combinations. The orbital combination in the left diagram overlap and can produce a stabilized bond orbital. The combination in the right diagram cannot produce a bond orbital because the orbitals do not overlap (Eint = 0).
The need for good orbital overlap (large Eint) also explains why covalent bonds are short. There is an energy "reward" (stabilization of BO) for creating good overlap. Summary. Bond orbitals necessarily involve overlapping atomic orbitals of similar energy. Orbital combinations that do not meet these two criteria cannot produce bond orbitals.
Hybrid orbitals are superpositions of two or more atomic orbitals on the same atom. Therefore, when we form a C sp3 orbital, the low energy 2s orbital corresponds to WF(I), the higher energy 2p orbital corresponds to WF(II), and the hybrid orbital corresponds to WFsuper: sp3 = 0.5 2s + 0.87 2p The energy analysis given above no longer applies because we have combined the atomic orbitals in an arbitrary fashion, rather than seeking an optimal combination. It is still the case, however, that the hybrid orbital's energy is calculated using a formula like: property(superposition) = propertywrong + interactions This formula can be simplified immediately because the interactions term is zero (orbital interactions are proportional to orbital overlap and atomic orbitals on the same atom do not overlap.) If we substitute "energy" for "property," we obtain: energy(superposition) = energywrong where energywrong is a weighted average of E(I) and E(II). The weighting coefficients are the squares of the n values: E(sp3) = (0.5)2 E(2s) + (0.87)2 E (2p) = 0.25 E(2s) + 0.75 E (2p) |