The Structure of a Wind Turbine's Vortex

A wind turbine mixes wind into chaotic vortices. These vortices limit efficiencies of the turbines that are located downstream. The tip of the turbine’s blade creates a particularly strong vortex. In the latter part of my research, I have become enthralled with how this vortex’s strength varies across space. This vortex is strongest near the middle of the vortex, and it is weaker farther away. Let us refer to the vortex’s strength as vorticity. Along a line that bisects the vortex, the plot of the vorticity versus the distance is similar to the plot of a Gaussian function, which also known as the normal distribution or the bell curve.
Thus, the vorticity distribution is approximately Gaussian. The reason for this Gaussian approximation is that diffusion smears the vortex out into a Gaussian shape. Diffusion often acts to spread distributions out into Gaussian curves; as you read this sentence, this process occurs around you because diffusion acts to spread heat out towards a Gaussian distribution. Gaussian distributions frequently occur under diffusion because Gaussian convolutions are mathematically simple ways of smoothing out functions. Diffusion spreads a vortex out to a stable, more uniform state by making the distribution into a progressively shorter and broader Gaussian.
Diffusion, however, is not the only force that acts upon a vortex; for interactions between vortices make the vorticity distribution more complicated than a simple Gaussian. A plot of vorticity along a line that bisects a vortex is similar to - yet distinctly different from - a Gaussian. Distributions across various lines differ from Gaussians in different ways. Averaging these plots together gives the graph shown below. The vorticity is normalized by the maximum vorticity of the vortex.
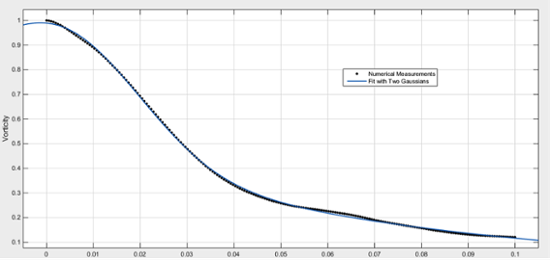
Distance from Vortex in Rotor Diameters.
This averaged distribution closely resembles the Gaussian curve. This heightened resemblance occurs because diffusion acts to spread the vorticity distribution into a Gaussian. When you average out the effect of diffusion, it does not cancel out, because it acts similarly everywhere. The other force that affects vorticity distribution, however, does acts differently at different places. This force regards the interactions between vortices. It depends on many parameters, such as the distance between vortices. Since this force depends on many different parameters, it can act in opposite ways at different places; thus, averaging can cancel its effect out. That is why the averaged vorticity distribution is more Gaussian than the distribution across a single line. A Gaussian curve is a good first approximation to the vorticity distribution, because the diffusion systematically brings the vorticity towards a Gaussian curve.
This approximation can be utilized in multiple ways. Outside of wind energy, many mathematical studies have researched how Gaussian vorticity distributions evolve in time. They have found that the time it takes for vortices to merge together depends on the vorticity distribution. If the wind turbine’s vortices are Gaussian, then we can use results from these studies to more effectively learn how the vortices evolve. Knowledge on vortex evolution can be used to limit the detrimental effects of vortices on wind turbines. Additionally, numerical simulations may be able to utilize Gaussian approximations in order to more efficiently study how vortices evolve. Current simulations track millions of grid points, which take a lot of computation. Instead, simulations might improve efficiencies by just tracking a relatively small number of vortices. Research upon vorticity distributions can illuminate characteristics of vortex merging, which, in turn, can be used to innovate wind farms.
Tags: psf, presidents summer fellowship, wind turbines, wind power, turbines
