How Much Does My House Cost???
Salma Huque
How Much Does My House Cost???
This article explores how different types of models compare when predicting on new data. In particular, I compared stepwise regression, bagging with random forests, and boosting. For each model I will explain the model building process and how the best model was selected. At the end of article, I will present comparisons of how the three models did on predicting completely new data. It’s a race to see which technique is best!
The Data
The data at our disposal is a beautiful dataset with information collected by the city of Portland’s Bureau of Planning and Sustainability. It was constructed and cleaned by Ryan Kobler and me! It contains property level observations for sales of single family residential homes sold in Portland, OR between January 1, 2014 and January 1, 2018. Each observation represents a property transaction and each variable represents a characteristic of the property. We have structural, neighborhood, and environmental characteristics, as well as the sale price for which it was sold. The benefits to using this dataset for machine learning is the large amount of observations as well as predictors. This allows the model to be fed more observations and get a better idea of the dataset. We will be using the characteristics to predict the sale price of a subset of these houses. While Ryan and I created a structurally clean dataset, the models I will use below work better with some additional love. I standardized each of the numeric variables that varied widely by subtracting each value by the variable’s mean and dividing by the variable’s standard deviation. This ensures that each numeric variable has a mean of 0 and a standard deviation of 1, which will help avoid giving too much power to a single extremely variable variable. In addition to standardization, I also dropped missing variables for tax lot area and building value and dropped any infinite values in the dataset. Leaving these in cause the models to crash.
My final dataset had 22,251 observations of 33 variables. Below is a glimpse of the data:
## Observations: 22,251
## Variables: 33
## $ STATE_ID <chr> "1S2E08CC 22700", "1S2E09CD 12000", "1S2E07CC 149…
## $ SITEZIP <dbl> 97206, 97266, 97206, 97206, 97266, 97206, 97206, 972…
## $ LANDVAL3 <dbl> -0.210521180, -0.185744431, 0.076253769, -0.21052118…
## $ BLDGVAL3 <dbl> 0.094666022, 0.276190243, -0.132973975, -0.222849314…
## $ TOTALVAL3 <dbl> -0.02078455, 0.12291120, -0.02849542, -0.21730496, -…
## $ SALEPRICE <dbl> 499900, 348000, 419500, 319000, 320000, 370000, 2800…
## $ age_sold <dbl> 91, 54, 67, 109, 59, 115, 96, 65, 62, 92, 29, 70, 11…
## $ totalsqft <dbl> 0.20077906, 0.08763998, -0.50919554, -0.30666280, 0.…
## $ taxlot_area <dbl> -0.89489983, 0.05271281, -0.23000991, -0.89489166, 0…
## $ f_baths <dbl> 2, 2, 1, 2, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 2, 1…
## $ h_baths <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ n_fireplaces <dbl> 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1…
## $ garage_dum <dbl> 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ deck_dum <dbl> 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1…
## $ attic_dum <dbl> 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0…
## $ bsmt_dum <dbl> 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1…
## $ percent_vacant <dbl> 0.1600000, 0.2666667, 0.2000000, 0.2089552, 0.400000…
## $ total_canopy_cov <dbl> -0.007681764, -0.369694912, -2.241625158, -1.6221726…
## $ zone_change <dbl> 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ CN_score <dbl> 0.254999917, 0.142121117, 0.224383475, 0.254999917, …
## $ dist_cityhall <dbl> -0.11370482, 0.12183205, -0.45141939, -0.14786237, 0…
## $ dist_ugb <dbl> 0.4183172, 0.3673226, 0.3751601, 0.4196334, 0.365589…
## $ conAirHgt <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conLSHA <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conSlp25 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conPubOwn <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conSewer <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conStorm <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conTranCap <dbl> 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conTranInt <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conTranSub <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0…
## $ conWater <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ conCovrly <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…Machine Learning
Machine learning is a term used for a broad selection of modeling techniques that involve two things: training and testing. Given a dataset, the observations are randomly split into two groups. Seventy-five percent go into a training group that is used to fit a model via a given technique. Then twenty-five go into a testing group that is used to gauge how good of a model the technique created. There are different ways to measure how good a model predicts new data, and I will use mean squared error (explained further below). Note that the 75-25% split is most common but can vary. Each of the following models were trained on the exact same training data sampled from the sales data. They were then trained on identical testing data pulled from the same sales data. This allows us to directly compare the predictive power of the three models. No observations are in both sets.
Model 1: Stepwise Regression
The first machine learning technique we explore is subset selection, and more specifically stepwise selection. There are two types of subset selection: best subset selection and stepwise selection. Best subset selection goes through every possible combination of predictors and compares them all to find the best one. However, this leads to my poor computer having to run 2p different models on a dataset with 33 predictors. The computational effort this takes is ridiculous, so most people have resorted to a sneakier method: stepwise regression.
Stepwise regression models are built by adding or subtracting predictors methodically to the model based on a predetermined set of criteria. There are two ways this can be done: forwards and backwards. Forward stepwise selection starts by picking the model that works best when there is only one possible predictor (say tax lot area). It then picks the model that works best with a combination of tax lot area and one other predictor. It continues this for all p, so that rather than 2p models, we instead only deal with p+1 models (the extra model being one with no predictors), each with a different number of predictors. From this subset, we can then select the best model. The “best” model is chosen based on a combination of AIC, BIC, and adjusted R2.
Backwards stepwise regression works the same way, but instead begins with a model containing all p predictors are iteratively removes the least useful predictors. I chose to use this way based on the model specification I used in my thesis, which included a whole ton of variables. However, both forward and backward stepwise selection have the same important problem: subsequent models are forced to include earlier predictors in their formulas. This is a problem if the best one-predictor model is X, but the best two-predictor model is Y + Z. Stepwise selection will never create the Y + Z model because X will be a predictor in all subsequent models.
Backwards stepwise regression led to using the following ten predictors:
Model 2: Bagging with Random Forests
The second machine learning technique we explore is bagging via random forests. Bagging and boosting (in the following section) both improve of the concept of a decision tree. A decision tree is a flowchart with internal “nodes,” each of which represent a test on a given variable. Depending on the response to the test, you move to a different branch of the tree and take more tests until you reach a final outcome. Decision trees are useful because they allow for more flexibility in the model that a regression as in the above model. However, individual trees trained on the same data suffer from high model variability; you will likely get a very different result every time you run the model.
Here is an example of a decision tree:
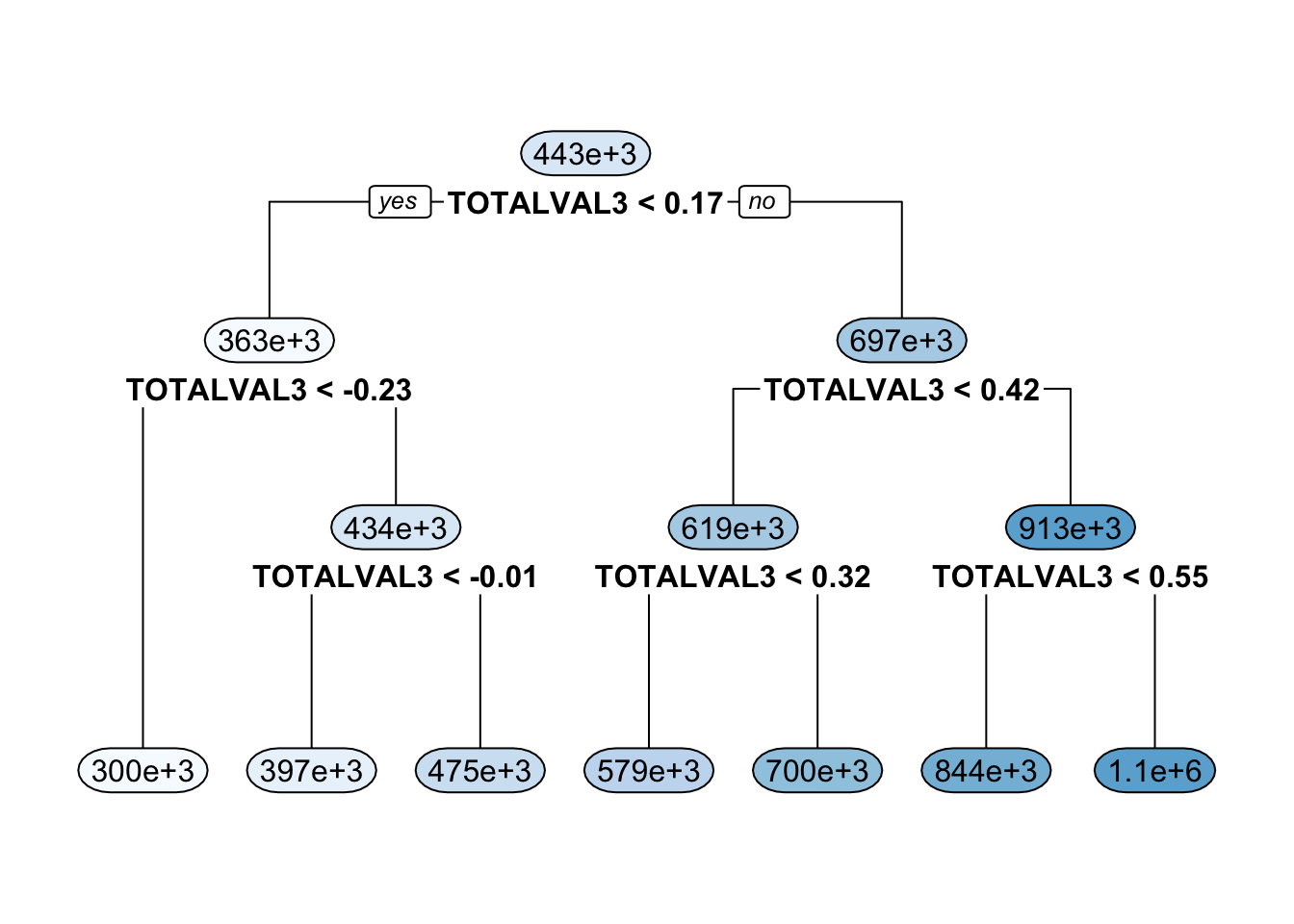
Bagging is a method of decreasing model variability by training many decision trees on the same data and then aggregating the results into a single tree. While model variability is undesirable, when aggregating trees, we want to maximize variability in order to get the most flexible model. Each decision tree in the set is trained on data bootstrapped from the original sample, which encourages variability between trees. Furthermore, with random forests, each node on a decision tree is chosen from a subset of the total number of predictors. The total number of trees created is usually upwards of 500, and the number of predictors tried at a given node is usually the square root of the total number of predictors.
After aggregating the trees into a single “best” decision tree, the model uses the test dataset to predict. Again, we will use mean squared error to gauge how well of a predictor random forests are for this dataset.
Model 3: Boosting
Similar to bagging, boosting is a process that also implements decision trees. However, rather that creating multiple trees and aggregating them into one, boosting takes one tree on a journey of self-discovery in order to help it improve over time.
Boosting involved iteratively changing the weighting of a dataset in order to turn it into a strong learner. First, a basic decision tree will be applied to the training dataset to create a model, then applied to the test data to create predictions. Any prediction error that results from this model will be given more attention in the next iteration. During the next iteration, a model will be fitted to a weighted version of the training set in order to reduce prediction error. This continues until a higher accuracy is achieved.
Like bagging, boosting helps reduce bias and increase variance in models. However, it has the added benefit of being able to better fit misclassified data as well as outliers.
Prediction & Conclusions
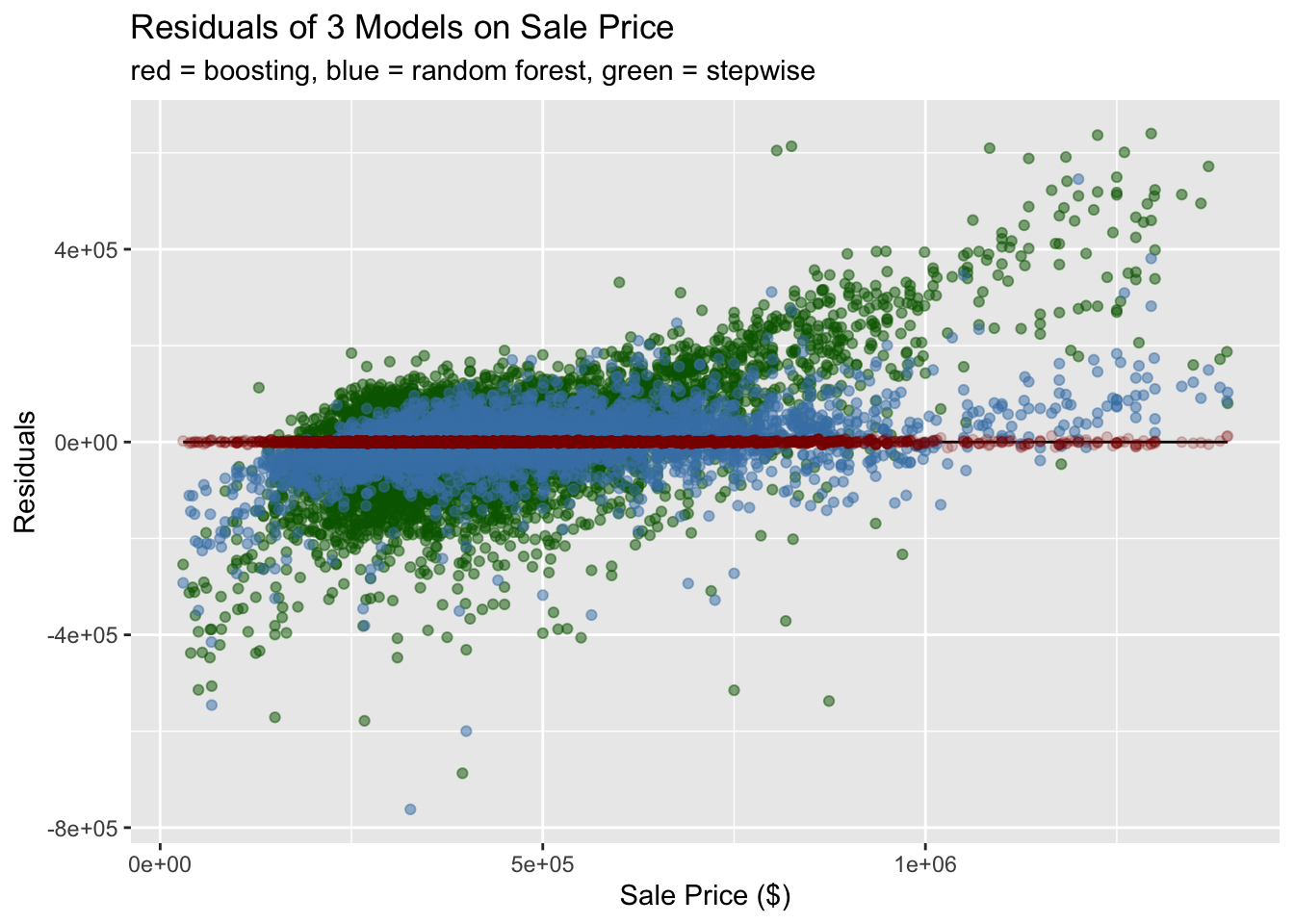
This graph shows the residuals of each model compared to the actual sale price. The true sale price is a horizontal line on zero, and residuals greater than zero were overestimates, while residuals less than zero were underestimates. We can see that boosting far and away had the best prediction of sale price. Furthermore, it had a low amount of variance at the tails of the data. In comparison, the random forest data tended to underestimate low sale prices and overestimate high sale prices, meaning it is less effective at extrapolating to new data. Finally, the stepwise function was a mess, and highly overestimated and underestimated and overestimated. It was the wost model.
Finally, I calculates the mean squared errors of each model’s predictive power. The results are below.
## Sale Price Stepwise Random Forest Boosting
## 0 13711594299 2686243869 1532197These MSE’s reflect the findings above: boosting is a super intense and amazingly powerful machine learning technique that is FAST. No wonder it won all those Kaggle competitions.
For more information about this dataset, read my thesis!!!
Sources
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An Introduction to Statistical Learning: with Applications in R. New York: Springer, 2013.