|

|
What
is electron density?
The theory of quantum mechanics says that an electron's position can only be described statistically. It also describes a method for calculating the probability of finding an electron at one point or another. This calculation produce a quantity called electron density, a number that tells us the relative probability of finding an electron at a particular point in space. Quantum mechanics also says that an electron can be viewed as a stationary wave, or, cloud of negative charge. According to this point of view, the electron density is a number that tells us how much charge is located at each point in the cloud. The following sections describe these ideas in more detail, beginning with the mathematical connection between wave functions (orbitals) and electron density.
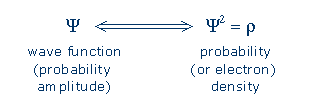
From wave function to electron density An electron's wave characteristics are described mathematically by its orbital or wave function, Y (Greek letter "psi"). A wave function assigns a number to each point in space, and the numbers oscillate so that they are positive at some locations and negative at others (this behavior may remind you of the way a water wave can make a lake's surface rise at some points and fall at others). The electron density function, r (Greek letter "rho"), is equal to Y2 [optional math note]. This guarantees that r (rho) will always have a positive value, and this value expresses the relative probability of finding an electron at a particular location.
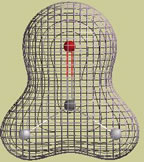
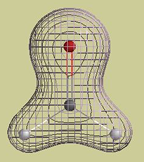
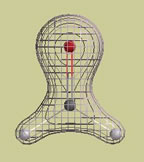
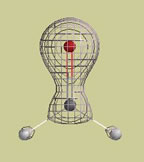
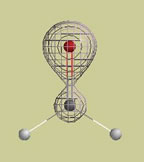
An example The following picture is a graph of the electron density in a water molecule. The graph consists of two surfaces, a "solid" inner surface and a "mesh" outer surface. Each surface is constructed so that r (rho) has the same value at every point on the surface.
This particular graph is constructed so that r (rho) is 10 times larger on the solid surface than on the mesh surface. In other words, if we randomly select one point (rsolid) on the solid surface and one point (rmesh) on the mesh surface, the value of r (rho) at rsolid is 10 times larger than the value at rmesh. Of course, this also means that it is 10 times more likely that an electron will be at rsolid than at rmesh. We can also compare the probabilities of finding electrons anywhere on each surface. The probability of finding an electron anywhere on a surface is proportional to r (rho) x A, the electron density multiplied by the area of the surface. It so happens that the area of the solid surface is about 2.5 times smaller than the area of the mesh surface. Therefore, it is only about 4 times more likely that an electron will be somewhere on the solid surface (4 = 10/2.5).
Electron density cloud A "particle" electron can also be described by a "wave" function or orbital. The orbital, whether atomic or molecular, covers a region of space and does not move. The orbital picture says, in effect, a moving electron looks like a stationary cloud of negative charge. We say the cloud is "stationary" because the amount of negative charge at each point does not change (remember: the orbital's shape does not change). The electron density tells us the relative amount of negative charge that is located at each point. Thinking back to our water molecule, we can now say that this molecule consists of three nuclei (two hydrogen nuclei and one oxygen nucleus) embedded in a single cloud of negative charge. The graph that I showed you provides some information about how the negative charge is distributed. Each point on the solid surface holds 10 times as much negative charge as each point on the mesh surface. However, the entire solid surface holds only about 4 times as much charge as the mesh surface.
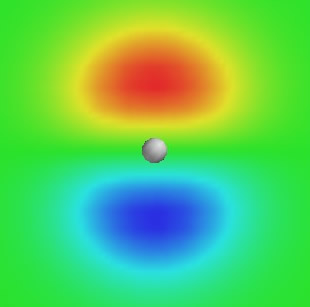
Review problems Take some time to review what you have learned on this page. #1. This graph describes a 2p electron, i.e., an electron assigned to a 2p orbital. The graph shows information gathered on a plane that cuts through the atom's nucleus (white ball). Numerical information is color-coded so that negative numbers are colored red/yellow, positive are colored blue, and anything close to zero is green. Does this graph show information about the electron's wave function or electron density? Explain.
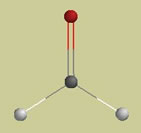
#2. Formaldehyde has the formula H2C=O. A molecular model looks like this (H = white, C = gray, O = red):
Four electron density graphs of this molecule are shown below. The same electron density is found at every point on each mesh surface (electron density, r (rho), and surface area, A, are listed on each picture). a. On which surface does each point hold the greatest negative charge? b. Which surface holds the greatest negative charge on its surface? c. Which surface contains the greatest negative charge inside its surface?
Optional math note. Warning: the following cautionary note is for the ultra-careful scientist. Here's the problem: r (rho) equals Y2 (psi-squared) only when a molecule (or atom) contains just one electron. If more electrons are present, a (slightly) more complicated formula must be used. The new formula makes r (rho) the relative probability of detecting any single electron out of the entire set regardless of where the other electrons happen to be. This is a subtle distinction and will probably never affect how you use r (rho) to think about chemistry, so feel free to forget about it. back |