
IRIS login | Reed College home Volume 94, No. 1: March 2015
Conquering the Number Plane

photo by Natalie Behring
Math major finds new way to pack polynomials
By Chris Lydgate ’90
Imagine you are the ticketmaster of a vast, Borgesian concert hall with an infinite number of seats, neatly arranged in rows and columns. Unfortunately, a mischievous hobgoblin has roped off a section of the auditorium with a velvet cord, putting it out of bounds. Guests are trickling in. How do you assign each guest to a seat of their own?
Okay, it’s a far-fetched scenario, but math major Maddie Brandt ’15 is the first person in history to solve it in her paper “Quadratic Packing Polynomials on Sectors of R2,” which she presented at a conference in January.
The problem of assigning guests to seats is directly related to the problem of mapping the non-negative integers (those friendly, deceptively familiar objects such as 0, 1, 2, 3, and their ilk) onto the coordinate plane (defined by pairs of integers such (0, 0), (0, 1), (0, 2), etc.—think of the game of Battleship). How do you map the integers to the coordinate pairs in such a way that you count all the pairs one after another, without skipping any?
Reed students meet this problem in Math 321, Real Analysis, and solve it with a packing polynomial—a formula that assigns (x, y) to an integer N. The standard solution, shown by Fueter and Pólya in 1923, is:
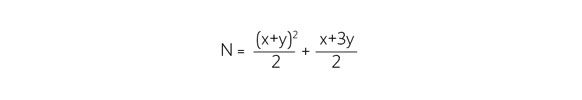
In Maddie’s paper, the problem is complicated by the rational sector—the hobgoblin’s velvet cord. She solved it by constructing K-stair polynomials.
Maddie came to Reed from St. Louis, Missouri, intending to major in physics. Then she took Math 332, Abstract Algebra, from Prof. Rao Potluri [1973–2014]. “I really loved that class,” she says. “It was like opening a doorway into a whole world. I got a taste for higher mathematics and I wanted more.”
The Reed math department is famous for its emphasis on understanding the why as well as the how. This approach can be challenging for students who just want to solve formulas, she says, but it has proven invaluable as she pursues mathematical ideas far beyond the reach of textbooks.
For her thesis with Prof. Angélica Osorno [2013–], Maddie is working on the Erdös-Ko-Rado theorem, an influential idea in the field of combinatorics, which bears on the following conundrum. Suppose that the world has n languages, and you wish to assemble a group of diplomats such that each diplomat speaks exactly k languages, and any two diplomats speak a common language. How many diplomats do you need?
Maddie is trying to find a new way to prove the EKR theorem by deriving it from a related idea known as the Baranyai theorem. So far, she’s discovered that a conjecture based on the Baranyai theorem, known as the wreath conjecture, does in fact lead to EKR. Proving the wreath conjecture, however, will be a major undertaking.
In addition to her polynomial pursuits, Maddie has worked at the Reed reactor, tutored in the math help center, and taken classes in ceramics. Last year she went to Budapest to study math and took a crash course in Hungarian (an experience she describes as “linguistic induction”).
Her paper won honorable mention for the Alice T. Schafer Mathematics Prize from the Association for Women in Mathematics, and she presented her findings at the Joint Mathematics Meetings, hosted by the Mathematical Association of America and the American Mathematical Society, in San Antonio, Texas.

LATEST COMMENTS
steve-jobs-1976 I knew Steve Jobs when he was on the second floor of Quincy. (Fall...
Utnapishtim - 2 weeks ago
Prof. Mason Drukman [political science 1964–70] This is gold, pure gold. God bless, Prof. Drukman.
puredog - 1 month ago
virginia-davis-1965 Such a good friend & compatriot in the day of Satyricon...
czarchasm - 4 months ago
John Peara Baba 1990 John died of a broken heart from losing his mom and then his...
kodachrome - 7 months ago
Carol Sawyer 1962 Who wrote this obit? I'm writing something about Carol Sawyer...
MsLaurie Pepper - 8 months ago
William W. Wissman MAT 1969 ...and THREE sisters. Sabra, the oldest, Mary, the middle, and...
riclf - 10 months ago