|
|

|
Chapter
4 – Electrostatic Potentials
Electrostatic potential Electrostatics is the part of physics that describes interactions between stationary charges. You are probably familiar with Coulomb’s Law, the central law of electrostatics. This law says that two charged particles exert a force on each other equal to: F = q1q2/r122 The electrostatic force, F, is proportional to the product of the charges on the two particles, q1 and q2, and inversely proportional to the square of the distance separating the particles, r12. Another important characteristic of a charged system is its potential energy, PE. Potential energy is created by electrostatic interactions between charge particles and is equal to: PE = q1q2/r12 Notice that this formula looks nearly the same as Coulomb’s Law. The only difference is that potential energy is inversely proportional to the distance between charges, while the Coulomb force is inversely proportional to the square of the distance. The most useful quantity for our purposes is the electrostatic potential. This quantity is related to PE as follows: the electrostatic potential created by a system of charges at a particular point in space, (x, y, z), is equal to the change in potential energy that occurs when a +1 ion is introduced at this point. This definition can be made clearer with the aid of the following pictures. Imagine a molecule consisting of an electron density cloud and several positively charged nuclei. We might represent the molecule by the following cartoon:
Now suppose we want to know the electrostatic potential this molecule creates at point (x, y, z). We can obtain the potential by introducing a +1 charge at (x, y, z) and calculating the change in energy. The new picture looks like this:
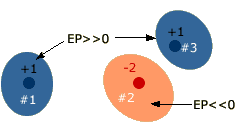
The change in energy is simply the potential energy created by interactions between the +1 charge and the charges in the molecule. We can calculate this energy by calculating (+1)(qmolecule)/r for each charge in the molecule, qmolecule, and adding up all of these energies. This energy is the molecule’s electrostatic potential. Electrostatic potential is both a molecular property and a spatial property. It depends on what charges exist in the molecule and how they there are distributed. It also depends on what point (x, y, z) we choose to investigate. If we select a point where the +1 charge is attracted by the molecule, the potential will be negative at this point. On the other hand, if we select a point where the +1 charge is repelled, the potential will be positive. Molecules contain many charged particles, nuclei and electrons, and the net impact of these particles on the +1 “probe” can only be determined by a computer. However, since we know that potential energy and distance are inversely related, it is likely that the molecular charge(s) closest to the +1 particle have the largest effect. For example, the following diagram shows an ionic compound consisting of three ions. It is likely that the potential in the immediate vicinity of each ion is determined largely by this ion, and the more distant ions have relatively small effect. On the other hand, the potential in any region that is near two or more ions must be determined by a careful calculation. Potential is large and positive in blue regions, and large and negative in pink region.
This kind of behavior is seen in practically every system. Positive particles, like atomic nuclei or polyatomic cations, are surrounded by regions of positive potential. Likewise, negative particles, like polyatomic anions, are surrounded by regions of negative potential. In a few pages I will show you how to use electrostatic potentials to make qualitative statements about atomic charges. When I do this, I will assume that the potential in a given region is controlled by the “local” atom, so a positive potential will indicate a positively charged “local” atom and a negative potential will indicate a negatively charged “local” atom. |